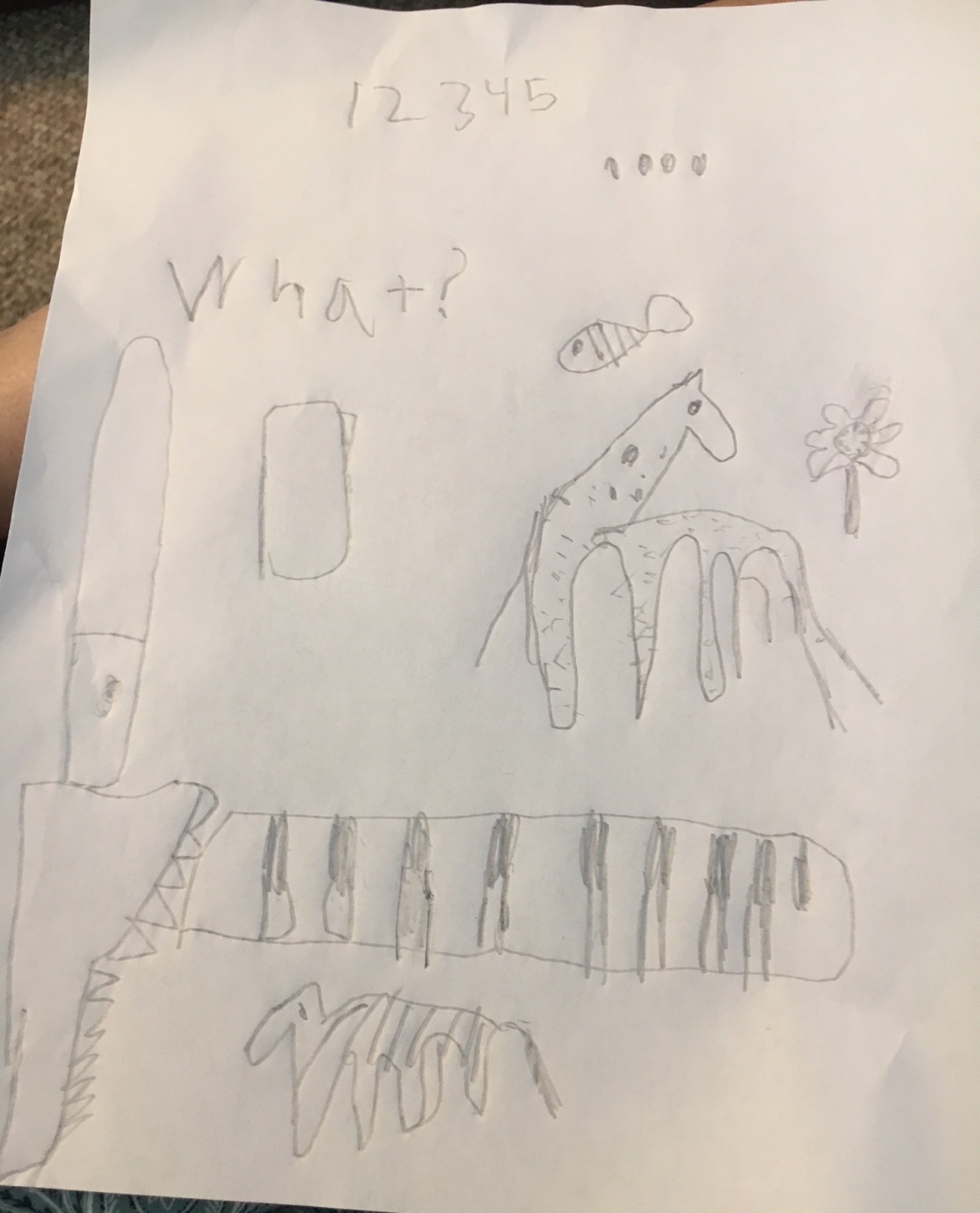Funville Adventures launched!

Funville Adventures, our math-inspired fantasy adventure with Allison Bishop, is officially published! It is available on amazon and directly from Natural Math, where you can read more about the book.

Here are some early reviews of the book:

“You too will want to visit Funville, a delightful land where magical and strangely mathematical powers run rampant!” – Jordan Ellenberg, author of How Not to be Wrong

“Mathematical words can sound scary, but the concepts they describe are not: Funville Adventures proves this so!” – James Tanton, MAA Mathematician at large

“Enjoy the story. Stay for the math. Emmy and Leo’s magical adventure will encourage families to play with ideas together.” – Denise Gaskins, author of Let’s Play Math series

 

7th Annual Main Line Math Festival

Our 7th annual Math Festival on the Philadelphia Main Line for children ages 5-12 is happening on October 22, 2023! It will take place at Main Line Classical Academy and is jointly sponsored by MLCA and Golden Key Enrichment.

If you’re in the area (or not too far from it 🙂 ), come and discover for yourself the joy and beauty of mathematics! Solve challenging puzzles, build tricky structures, learn fascinating magic tricks, create colorful symmetrical artwork, play games, and most importantly, have fun! Volunteer opportunities for interested high school students (community service credit can be provided)!

This event is free for all attendees. However, registration is required – please use the RSVP link to register in advance so we can be prepared for the right number of participants!

REGISTER HERE: https://forms.gle/uCYES626Tf2qAqQbA

Find out more about the festival on the FB event page: https://fb.me/e/1sdUJ6DC0

And here are some more pictures from last year’s event:

How Many? – A book and a math adventure

It was a rainy day in the middle of summer vacation. Ben and Zoe (6 and 5 yo) were home together because they were too young to join their older siblings on their adventure. They were a little sad and not sure what to do.

“Let’s do some math,” Zoe’s mom suggested.
“Okay…” they agreed somewhat reluctantly.
“But no pluses or minuses,” said Zoe.
“I like multiplication,” chimed Ben.

“I have an idea,” said mom and took out a book that Zoe and Ben had never seen before.
“How many?” Ben read the cover. “I know,” he said. “It’s a fraction book.”
“Why do you think that?” asked Zoe’s mom.
“Because I saw the back of the book,” Ben explained.

“I guess we’ll see,” said Zoe’s mom and opened the book.

On the inside cover there was a picture.

“How many?” asked Zoe’s mom.
“How many apples?” Ben replied with a question of his own.
But Zoe was already busy counting away. Before Ben or mom could say anything else, Zoe exclaimed, “Nine!”
Ben looked at the picture again. “No, it’s eight,” he said. “Look, it’s three, three, and two,” he continued, pointing to groups of apple pieces.
“But you forgot the middle piece,” countered Zoe.
“That one doesn’t count.”
“Yes it does,” insisted Zoe.
“No, it doesn’t, because you don’t eat it,” Ben explained.
At this point they both looked at mom, expecting her to settle the dispute.
“You’re both right,” she said. That caused some confused looks. “Well, I didn’t say how many what, so you can count whatever you want.” The confusion turned to excitement.
“Then I can count apples,” Ben said. “There’s one apple. And I know what that other thing is. It’s an apple cutter, and there’s one of those. I’ve seen them before and they’re really cool.”

Once they felt like they were done with both sides of the cover, they decided to continue exploring the book. On the next few pages, they had some fun conversations involving shoes, laces, eggs, cartons, dozens, omelets, yolks, and more. They then came to this page.

“How many?” mom asked.
Ben said, “12 grapefruits.”
“No, these are halves,” said Zoe.
“They’re not halves,” insisted Ben. “They’re fractions, but not halves.”
“What fraction do you think they are?” asked mom carefully.
“I don’t know, eighths?”
“So you think that eight of them make a whole grapefruit?”
“No. Two of them do. But they’re still not halves,” said Ben, almost mysteriously.
Meanwhile, Zoe paired up the “not halves” with her fingers and announced that there are six grapefruits. Ben agreed with that analysis and added that there is one cup and one green thing. Mom explained that the green thing is called a squeezer. “Oh, it’s to make juice,” said Ben excitedly.

This nicely foreshadowed the next page on which they had a discussion about squeezing the grapefruits, taking out the seeds, measuring the amount of juice, and drinking it.

And then came the avocados.

Ben quickly looked at the picture and declared that there were 15 avocados.
“No, those are not whole avocados,” Zoe disagreed.
“Ah, we need to divide by 2 to get the number of whole avocados,” said Ben. “But wait, 15 cannot be divided by 2. I told you it was a book about fractions!”
But Zoe was already doing her usual thing of pairing up the “halves” with her fingers.
“There are seven and a half avocados,” she declared.
“What do you think they did with the other half?” asked mom.
“They squeezed it!” exclaimed Ben.

And so they continued, page after page. Many heated discussions were had, about eggs, pizza, pies, utensils, shoes, and so much more!

And when every page was flipped and the back cover was done with, but Ben and Zoe kept requesting more, mom suggested that they each make one of their own for her and for each other.

The kids happily agreed. Ben drew his very quickly, but then kept adding more things to it. It had the extra challenge of figuring out the “what?” in addition to the “how many?”

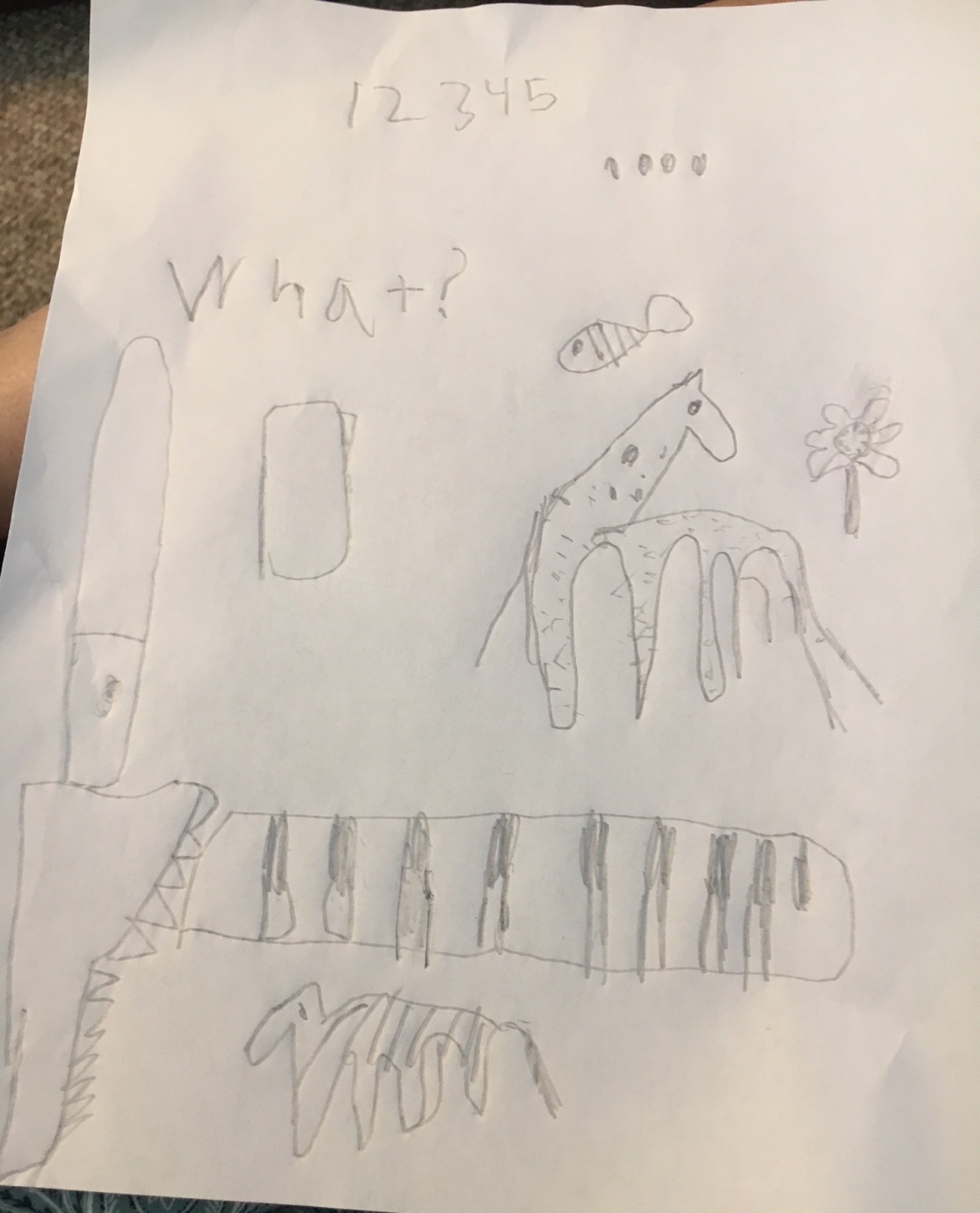
Zoe kept starting over, but finally also came up with something she was happy with. Those funny letters spell the word for “how many?” in Russian.

Zoe’s mom had a lot of fun answering their questions of “how many?” Now it’s your turn to play!

This adventure was made possible by the How Many? book by Christopher Danielson.

 

Naming Numbers at Bedtime

Setting: I am putting Zoe (5 yo) to bed.

Z: Mom, what comes after one hundred?
Me: One hundred and one.
Z: No, I mean when you’re counting by tens.
Me: One hundred and ten.
Z: But then what comes after one hundred ninety?
Me: Two hundred.
Z: But what comes after nine hundred?
Me: Nine hundred and one.
Z: But by tens.
Me: Nine hundred and ten.
Z: So what comes after nine hundred ninety by tens?
Me: One thousand.

This conversation continued for a very long time, with questions about what comes after one thousand, one thousand ten, one thousand ninety, one thousand one hundred, and so on. I understood fairly quickly that when she asked “what comes after…?” she really wanted to know the name of the next order of magnitude. But for a while I answered her questions very exactly and made her figure out a way to get precisely to what she wanted to know (yes, I can be cruel to my children like that).

In this way, it took her quite a few questions to get to a million, but she did get there eventually. In fact, when she got there she was surprised that a million was bigger than a thousand because I think that she hears the word million much more often somehow.

After that, I took pity on her and told her the words for billion, trillion, quadrillion, and a few more.

Z: So when do we get to googol and googol plex?

I told Zoe that a googol, and especially googol plex don’t come for a while and that there aren’t “names” for all the numbers up to googol plex. She gave me a very confused look and asked, “But don’t numbers go on forever?” I told her that while numbers go on forever, words do not.

This left her pondering for long enough to finally fall asleep. But something tells me that the conversation is not really over…

Main Line Math Festival on April 22

On April 22, Golden Key Russian School and Main Line Classical Academy are hosting their fifth Main Line Math Festival for kids ages 5-12.

Date: Sunday, April 22
Time: 4 PM – 6 PM
Location: Temple Brith Achim, 481 S Gulph Rd, King of Prussia, PA 19406

For more details and to register visit the festival site.

To find out what you can expect, read about previous festivals here and here.

Stations will include:
-Discover the One Cut Theorem
-Building Extravaganza using newspaper rolls, Kapla Blocks, chickpeas+toothpicks
-Explore symmetry through various math and art projects
-Logic puzzles galore
-“Guess my rule” Function Machine
-Paper folding problems
-And more!

Here are some pictures from previous festivals:

Funville Adventures is on a Web Tour!

Through March 15, Funville Adventures will be visiting blogs, forums, and other communities throughout the web.

Today, the tour had its first stop at Talking Math With Your Kids by Christopher Danielson.  The title of his post is Things that Give me Hope and in it Danielson lists some of his favorite math projects, including Funville! I could tell you what the others are, but I  want you to read the post; it is beautifully written and inspiring.

More details about the tour and coming attractions can be found here.

If you have a web page, a blog, a podcast, a community, or another way to share mathematics, we would like to invite you to take part in the Funville web tour. Please email reach.out@naturalmath.com to join the adventure!

Don’t have any of those but still want to participate? Send us your stories, quotes, and fan art and we will feature them on the site!  Or you can write a review here or here.

 

Secret 3-digit numbers

For the past two weeks, in my first grade math class, we had been playing with 3-digit numbers. Many of the students in this class are the same ones that participated in the lessons described in the posts 3-digit numbers are tricky!, Part I and Part II, from last year.

But now, 3-digit numbers are their old friends and they are ready to do much more sophisticated things with them. I have found a number of interesting activities in the Super Source – Base Ten Blocks book for grades K-2 for us to try out.

One of the activities was a particular hit with the students. Here is how it worked.

One student would go to the special table and build a 3-digit number inside a box using base-10 blocks. That student would then give out clues about the number until another student built the same number.

Here are lists of clues that three different students came up with. Can you guess the numbers? For reference, a unit is 1 little cube, a rod consists of 10 such cubes and a flat consists of 100 cubes.

Student 1:
Clue 1: The number of units is 1
Clue 2: My number is bigger than 100 and smaller than 500
Clue 3: The number of tens in the flats is 40.
Clue 4: There is only 1 rod.

Student 2:
Clue 1: There are 9 flats.
Clue 2: There are 14 blocks total.
Clue 3: The number is bigger than 909.
Clue 4: The number of rods is smaller than 6.
Clue 5: There are 5 units.

Student 3:
Clue 1: The number of units is smaller than 9.
Clue 2: There are 20 blocks altogether.
Clue 3: The number of flats is smaller than 7.
Clue 4: The number of rods is smaller than 7.

Notice that both Student 1 and Student 2 have redundant clues, which was very typical. But it was the clues of Student 3 that I found particularly interesting.
It was not immediately obvious, even to me, that they were sufficient to determine the number.

The “guessing students” took some time after Clue 4 to come up with a number that fit all 4 clues, but to my surprise they all came up with the same number, which turned out to be the correct one. Only then did I realize that the clues were in fact sufficient.

I tried to discuss this fact with the students, but I’m not sure that they followed much of what I said. They were excited to have guessed the number and the next student wanted their turn at the special table.

What are your favorite 3-digit number activities to do with this age group?

 

Witnessing the woes of math homework

Every week, I spend several hours in the waiting area of a large gym where my kids take gymnastics lessons.  The room has several large tables where parents and siblings can do their work while waiting for their gymnasts.

Many kids use this time to do their homework and by far the most common subject that I see them working on is math.  About half the time, the parents are helping them.  The kids rarely look excited but they are generally resigned.

Last week, I witnessed a scene that left me very disturbed. A mom was helping her daughter, who looked to be about 9 or 10, with math homework. The girl would alternate between crying, yelling, or even occasionally hitting the mom. She also kept repeating the following phrases, “I don’t understand this,” “You are wasting my time,” and “I hate you/this.”

The mom was generally much calmer than I would expect someone to be in this situation. Her most common response was, “Sweetie, you just have to memorize that this is the way you do it.” When she was explaining something, all I would hear is, “You have to put this here,” and “You have to write this there.”

At some point, the mom said, “It’s ridiculous that they’re having you do this. I didn’t have to do this sort of thing until college.” I don’t know what this specifically referred to, but later, I did overhear the mom reading a different problem to the daughter and it was definitely not anything beyond standard third grade level.

This all went on for over an hour. There were moments when I was very tempted to come over and offer my help, but I couldn’t bring myself to do it and wasn’t sure that it would be appropriate.

I know that math anxiety exists – I’ve seen it. I’ve also witnessed bad parent/child interactions. But this prolonged scene really staggered my imagination.

And now a few questions for the audience. How common is this? Are there many kids out there crying over math homework for hours? Is this hurting their relationship with parents who are trying really hard but for one reason or another are not able to help them?

And on a more specific note, should I have tried to help somehow in this particular case? Would you have?

 

 

The mathematical boundary between a joke and a lie

Like all siblings, my children occasionally quarrel. I generally try not to get involved unless it gets loud or one of them complains to me. Sometimes, however, I hear something that amuses me and I tune in or even join the conversation.

Today, it began with Zoe (5 yo) accusing Katie (9 yo) of lying to her. Katie, in her turn, was claiming that it was just a joke. This is how the conversation continued:

Katie: You don’t even know the difference between a joke and a lie.
Zoe: Yes I do.
K: Oh yeah, what is it?
Z: For example, if you say “I ate 100 crepes”, then that’s obviously a joke. But if you say “I ate all the remaining crepes”, then that’s either the truth or a lie.
K: That depends on how many crepes were left.

This is where I joined the conversation. I was very intrigued to find out exactly at which point the joke turns into a lie. So I started asking some questions of my own.

The girls agreed that at 50 crepes it was still a joke and at 5 crepes it was a lie (assuming you didn’t actually eat them). When I asked about 20 crepes, there was a brief pause, and then Katie said, “You have to know the person.”

So the mathematical boundary between a joke and a lie, like so many other things, depends on the person.

Highlights of 2017

2017 was a very exciting year for me. Here are some highlights in three categories.

Teaching

This has been my first full (calendar) year of teaching. The first words that come to mind when I think about teaching are “wonderful” and “amazing”, but “hectic” and “stressful” are close seconds. That being said, I feel extremely fortunate to have found something I feel so passionate about and to work with awesome kids on a daily basis.

Book

This year I became a published author. The excitement of holding my first published book in my hands compared only to that of holding my newborn baby. The main difference is that with a baby your initial concerns are all about protecting it from “the world” while with a book they are quite the opposite – how to get it out there (and in the spirit of getting it out there, here’s the link where you can get it or write a review 🙂 ).

Family

Zoe started Kindergarten this year and Katie entered 4th grade. Although I post about them much more rarely than I used to, we still have many exciting conversations on a variety of topics. They both like math, but they also have a number of other interests: gymnastics, singing, piano playing, and Harry Potter topping the list. And then there’s my husband, who supports us in all of our crazy endeavors 🙂

I am looking forward to continuing these projects in 2018 and perhaps adding to the collection 🙂

Happy New Year!

Discovering the area of a trapezoid

Below is a guest post by Dmitry Bryazgin (originally written in Russian). Dmitry runs a small math circle near Princeton for students in grades 3-5. On the particular day described in the post, there were 4 students present.

The main task for the day was to find a general formula for the area of a trapezoid. The class had previously derived formulas for the areas of a rectangle, right triangle, acute triangle, and parallelogram.

For some additional motivation, I promised to give a prize to anyone who independently solves the problem.  I then drew all the previous area formulas that we had encountered and reminded the students of how we had derived them.  

Each student received a piece of graph paper and a pencil, and the search began.

The children puffed, cutting corners off and drawing all sorts of add-ons to the trapezoid.  I allowed them to use the board if they thought that would help them.  Some of the kids rushed to the board, but this did not lead to any progress on the problem.

Then I gave them the first hint: try to complete the trapezoid to a parallelogram because we already know how it find the area of the latter. This did not help.

Soon I started to notice that the students were getting tired, so I decided to give them a second hint: try to add a second, upside down, trapezoid to the original one.

The students once again took to their drawings and soon started to yell that they solved the problem.  But a quick check of their work revealed that the solution was not yet in sight.  Nonetheless, I was pleased to see that the children were not giving up and were showing a real interest in the problem’s solution.

At one point I realized that one of the students was close to the first step of the problem – the construction of the parallelogram – but the drawing on his paper was very small.

So I drew a grid on the board with a trapezoid on top of it and asked the student to show his construction. He came up and accurately transferred his drawing. This was the first successful step towards solving the problem. And then came the most interesting part.

I said that now we need to make that next step and find that “general formula”. The formula for the area of a parallelogram was written slightly higher on the board. Applying it required a substantial leap inside a child’s mind: realizing that the formula could be used for a DIFFERENT picture and understanding where in this new picture are the sides “a” and “b”. This, by the way, is already an abstract reasoning skill.

I pointed to the lower base of the trapezoid and asked the students for its length – all the answers were incorrect. I gave the students some time to think and then asked the question again. And suddenly, one girl exclaimed, “it’s a+b since we have the upside down trapezoid!”

If I could have have leaped to the heavens, I probably would have done so. I was really waiting for this answer, but had started to lose hope. After this, two other girls almost simultaneously exclaimed that we need to multiply by this by “h” since we have a parallelogram. And the student who had made the first step now added the finishing touch by pointing out that we need to divide by 2, since the parallelogram contains two identical trapezoids.

Until the very last moment, I did not know whether we would be able to solve this problem with the students.  This unpredictability of the lesson is what made it so interesting and what I wanted to share that with you.

By the way, no one ended up getting the prize, but it seemed that this was no longer important.

Afterthoughts

Looking back at the lesson, I thought of two mistakes/improvements that would have simplified the task for the students.

Mistake #1: I should have had the students draw a specific trapezoid on their papers with given dimensions. Without this, everyone ended up drawing whatever they wanted, the trapezoids were crooked and this got in the way.

Mistake #2: I initially did not draw the parallelogram on the board, whereas this was the key to solving the problem. I should have drawn it on a grid, along with the trapezoid, and had the students transfer both to their papers. Only after this should the search for the area have begun.